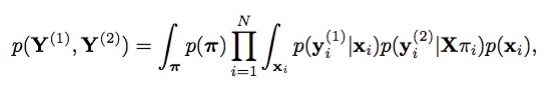Research
My research is focused towards building probabilistic models of data to provides means for us to reason intelligently and make decisions based on observations, more popularly known as Machine Learning. Intelligence can roughly be seen as the capability to reason under uncertainty, if we are completely certain about the state of the world then, as Laplace stated, the world is “an open book” and things becomes much less interesting, at least in terms of understanding while maybe not from an application perspective. But as an academic understanding a problem is much more important than solving it. Bayesian methodology formulates how we should reason in scenarios of uncertainty and provides means of how previous knowledge should be incorporated with data to update our beliefs in a principled manner. To again quote Laplace, “It is remarkable that a science which began with the consideration of games of chance should have become the most important object of human knowledge.” (Théorie analytique des probabilités. 1814).
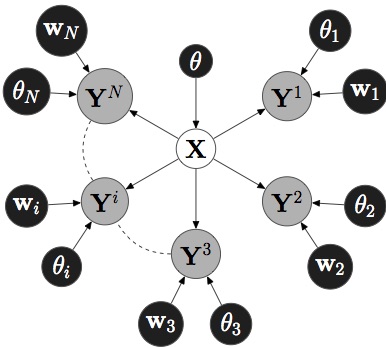
Multi-view modelling and factorised latent variable models
Many modelling scenarios are characterised by high-dimensional data from multiple simultaneous observation streams. Each stream corresponds to a different view of some underlying variate and can both provide complementary but also unique information. The complementary, or shared, information connects the information from several views while the unique, or private, variations provide information which is unique to a specific stream. When performing inference it is desirable to use all the available information, both those which are shared as it reduces uncertainty and the private which provides additional information to help disambiguate the current state. We have developed models that are capable of learning factorised latent representations that structures the latent space into separate parts containing shared and private information. In essence this allows for feature selection in a generative model, as the likelihood of a view is only effected by the portion that actually contains its variance. This allows for efficient inference and ambiguity modelling among other things. We have developed models using both Gaussian process priors and Dirichlet processes with the same structured philosopy.
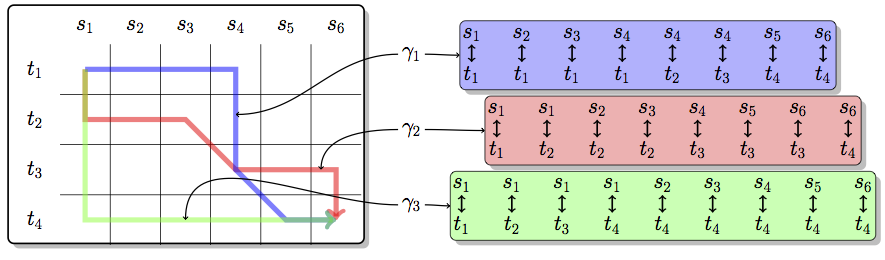
Alignments
Shared factorised latent variable models are able to discover correspondences between different views of the same data, thereby learning more intuitive representations that are capable of segmenting variations providing means for both exploratory data analysis, intuitive generation of novel data and efficient inference even in ambiguous scenarios. However, all these models make an assumption that the data is aligned, i.e. that there is correspondence between the points in each view. This is a strong assumption, as different alignments would lead to completely different representations. In many scenarios we do not know the correspondence between the data-points and this uncertainty should be included in the multi-view model. Furthermore, discovering an efficient explicit alignment is in many scenarios the ultimate task, for example when trying to solve correspondence problems. However, discovering an alignment means that we need to search over the space of all possible permutations of the data-points. In practice this is unfeasible as the number of possible alignments grows super-exponentially with the number of data-points.
Representation of structure
Many types of data have inherent sequential structure. Sequences of letters in computational linguistics, series of images in computer vision or cell structures in computational biology and arbitrary data sets depending on a parameter such as time provide familiar examples of such data. Commonly we avoid respecting this structure when we represent data and use techniques such as ‘Bag-of-Words’ style descriptors to circumvent the problem of not having vectorial input. This throws away a significant portion of the interesting variations for many types of data. We try to develop methods that are capable of exploiting this structure.